
"From
Simple to Complex"
Modeling and Optimization Strategy
The approach we use for creating MPT system model can be described as the following steps:
1. Small submodels creation
| Represent complex fermentative, transport etc. process as a system of
elementary ( first order) reactions, e.g. associations/dissociations, and
transformations. In such a way reactions like a calcium uniport,
respiratory complex I functioning, glutathione peroxidase work could be
modeled. Submodel approximation level depends on the it's role in the whole
model system - more important system part could be modeled in more details. For example, 2-substrate 1-product reaction will look in the following way: 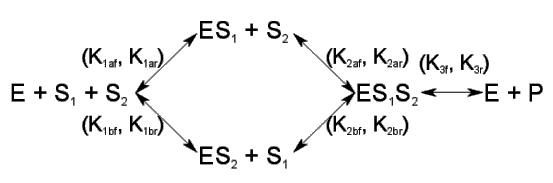 This representation is unified for all reactions and convenient for estimation in matrix-handling programs, like MatLab. Assign reaction constants and substances amounts (from the experimental
data or by model fitting)
| (An alternative approach, which is in development now: representing
reactions as complex processes with predefined kinetics, e.g. substrate
inhibition, reversible Hill's kinetics etc. It is more convenient, but less
precise approach.)
| Submodel optimization according to experimental data - fitting to
experimentally defined system parameters' values, dependencies and change
with time.
| Submodel behavior analysis - stability range and states analysis,
bifurcation points, oscillation regimes etc. | |
2. Larger models compilation
| Small submodels are compiled into bigger ones. In this way
several-reactions models are formed, e.g. calcium transport system (i.e.
system consisting of calcium uniport & Ca/Na exchange & Ca buffering
in mitochondrial matrix), respiratory chain model, mitochondrial
free-radical defense system (GSH-peroxidase & GSSG-reductase &
GSH-transferase & PN-transhydrogenase & PN-dependent dehydrogenases
etc.). Below you can see submodel of main processes of mitochondrial free-radical defense system:  Growing models should be optimized (in accordance to experimental data)
after each small submodels addition. | Here is general scheme fragment including parts of free-radical defense, Pi-transport and calcium transport systems: 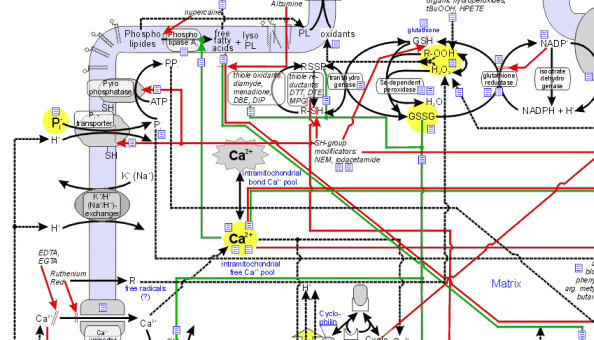 Several-reactions models, after optimization, are compiled into the general model of the
process: | General model optimization according to experimental data.
| "Numerical experiments" with the general model: | Possibly, big complex models should not be completely analyzed in a usual way (complete stability and states analysis, bifurcation points finding etc.) due to huge number of components. We can use rather "numerical experiment", when we observe behavior of the given complex system in prescribed conditions, and are able to change any parameter in some range (defined from submodels optimization and analysis, according to the real system) to change system behavior and define control coefficients. |
