MATHEMATICAL MODELING OF ENERGY COUPLING IN MITOCHONDRIA IN FRAMES OF PROTON-CHEMICAL HYPOTHESIS.
V.V.Lemeshko#,
A.G.Anishkin*.
*
Biology Research Institute of Kharkov State University, 310077,
Kharkov, Svobodi sq., 4, Ukraine.
# National University of Colombia, Medellin, Colombia.
The dependence of ATP-synthesis and mitochondria respiration rates on membrane potential is analyzed in frames of proton-chemical hypothesis of oxidative phosphorylation. The mathematical and electrical models of the unit of energy coupling are proposed. Computer analysis of the mathematical model allowed to obtain the theoretical dependences of the rates of ATP synthesis and of the respiration on membrane potential that are in good qualitative agreement with experimental data, contradicting chemiosmotic hypothesis.
Mitchell's chemiosmotic hypothesis [1] is commonly accepted for the description of the mechanism of energy coupling in biomembranes [2]. However, by present time the significant number of experimental data was accumulated that do not agree or obviously run counter to this hypothesis [3 - 9] and have caused the series of its modifications [10, 11, 12]. The chemical hypothesis of oxidative phosphorylation [4] was also improved in such a manner that though the availability of Mitchell's protonmotive force (DmH+) on coupling membrane was admitted, its minor role was ascribed.
Among main facts, which are difficult to explain in frames of chemiosmotic hypothesis, it is worth notice, in particular, the following:
1. Rate of oxidative phosphorylation as the function of membrane potential depends on the way of its change [3, 4, and 6].
2. Degree of mitochondrial respiration activation depends on way of reduction of protonmotive force magnitude on the same value [3, 9].
According to the chemiosmotic hypothesis, both the rate of oxidative phosphorylation and the intensity of respiration depend on the DmH+ magnitude, but not on the way of its change.
The satisfactory explanation of the above mentioned and number of other data, describing oxidative phosphorylation system, can be derived from the proton-chemical hypothesis [13 - 16]. The latter includes in a consistent way both chemical hypothesis and the elements of chemiosmotic hypothesis.
The purpose of the present work was the development of a mathematical model for quantitative description of interrelation between the rate of ATP synthesis and magnitude of DmH+, that can be changed by uncoupler, by oxidation substrate or by inhibitor of respiration.
ELECTRICAL AND MATHEMATICAL MODELS OF PROTON-CHEMICAL COUPLING
The mathematical model is based on equivalent electrical circuit of one proton-chemical coupling unit in respiratory chain of mitochondria [16]. The simulation of energy coupling by means of equivalent electrical circuits was numerously used by different authors as the method of qualitative and quantitative analysis of oxidative phosphorylation hypotheses [11, 12, 16]. For simplification of description of one coupling unit equivalent electrical circuit, we emphasize two main theses, following from proton-chemical hypotheses [13-16]:
1. Electron flux in the coupling unit divided in two and can pass not only by Mitchell's way, when the energy of difference of redox potentials is spent on transmembrane carrying of protons, but also by way of ATP chemosynthesis.
2. In mitochondria, the act of synthesis of one ATP molecule requires the transmembrane transfer of proton through ATP-synthase in matrix, and also transfer through ATP-synthase of two atoms of hydrogen (two electrons with two protons) from donor to acceptor of electrons in respiratory chain. These two processes are coupled in such a manner that the mechanism of ATP synthesis has the chemical nature, but also includes use of DmH+ energy. Besides, the energy of transmembrane carrying of one more proton is spent (in account per one molecule of ATP synthesized) on transport of phosphorylation substrates through mitochondrial membrane.
Thus, synthesis of one ATP molecule requires the energy of transmembrane carrying of two protons and energy of carrying of two atoms of hydrogen between redox-centers. Therefore, the summation of energy takes place, and this defines the magnitude of phosphate potential DGp, which can be created in the system:
![]() ,
,
Where F - Faraday constant, DmH+ - membrane electrochemical potential of hydrogen ions (Mitchell's protonmotive force), DE - difference of redox potentials in one coupling unit.
Let us consider mitochondrial proton-chemical unit of coupling in detail (fig. 1). In the scheme, the unit of coupling is divided on two subunits - "a" and "b", according to [16]. In subunit "a", the transfer of electrons is coupled only with pumping out of protons from mitochondria. But in subunit "b", the bifurcation of electron flux takes place: on Mitchell's flux, coupled with pumping out of protons, and on chemical, coupled with ATP synthesis and transfer of two protons in matrix. The simple account gives the stoichiometry 4H+/2e- per one coupling unit (subunit "a" plus subunit "b"), when there is no synthesis of ATP, and 1ATP/2e- per one coupling unit at completely coupled synthesis of ATP.
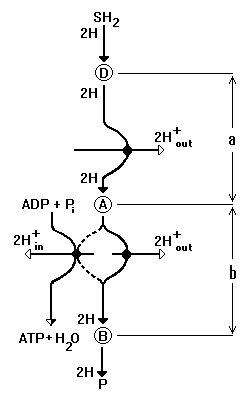 |
Fig. 1. General scheme of coupling unit. Symbols: D,B,A - redox-centers of respiratory chain;
|
Therefore, the synthesis of one ATP molecule in the coupling unit consumes energy, released at the transfer of two electrons by chemical way, and energy of transmembrane transfer of two protons.
Phosphite-thyole mechanism of oxidative phosphorylation was previously offered as one of possible variants of protonchemical coupling [13, 14, 16]. From this mechanism follows, that the rate of ATP synthesis is exponentially reduced at the reduction of membrane potential and difference of redox potentials between appropriate donor and acceptor of electrons in coupling unit [16]:
|
Where ![]() and
and ![]() - concentration of
phosphite and phosphate, respectively.
- concentration of
phosphite and phosphate, respectively.
Certainly, total reduction of phosphate to phosphite is considerably energetically unprofitable reaction [18] in view of very low redox-potential of this redox-pair [16], that makes the probability of participation of phosphite in mechanism of transformation of energy rather small, but does not exclude completely. At the same time, just based of hypothetical phosphite mechanism the general principle of proton-chemical coupling [16] is the most simply entered. Therefore, in analogy with formula (1), the exponential nature of ATP synthesis rate dependence on DmH+ and DEBA is also the result of any other redox mechanism of ATP synthesis in proton-chemical coupling unit, including one-electron and free-radical mechanisms [15].
In addition, "radical hypothesis" was offered later by other authors [19]. According to this hypothesis, the role of high-energy intermediate can be performed by cardiolipin, which is converted to cardiolipin enolphosphate in course of the redox reaction.
In the most general kind in frames of proton-chemical principle of coupling the distribution of electron flow between chemiosmotic and chemical branches of subunit "b", that determinates the rate of ATP synthesis, it is possible to describe as follows: when the coupling membrane have been maximal charged on chemiosmotic way, current through membrane (that is the sort of condenser) stops to proceed, and difference of redox-potentials DEBA in subunit "b" becomes also maximal one. All this is the reason of activation of electron transfer on chemical way. Thus, the mechanism of switching is thermodynamic one. In frames of this general mechanism some particular molecular mechanism of switching can exists, for example one of the mechanisms of regulatory effect of transmembrane electrical potential on functional activity of biomembranes, described by Konev and Kaler [17].
The equivalent electrical circuit (fig. 2), corresponding to one unit of proton-chemical coupling (in accordance to [16] (fig. 1)), can be presented as five circuits (fig. 2). The flux of electrons, in the form of a hydrogen atoms flux, from donor D to acceptor B (see fig. 1), is caused by appropriate difference of redox potentials (DEBD), which is the driving force of the oxidative phosphorylation process as a whole. On the equivalent electrical circuit (fig. 2) current in circuit I corresponds to the electron flux through the whole coupling unit, and the source of voltage Eo, with internal resistance ro, reflects the stationary difference of redox potentials DEBD between D and B. The stationary difference of redox potentials (DEAD), is established in subunit "a" and is reflected in circuit I as the source of voltage ea.
|
Fig. 2. Equivalent electric circuit of general coupling point. See commentary in the text. |
Appropriate difference of redox potentials in subunit "b" (DEBA) is reflected as the source of voltage eb. The value of current J in circuit I is equal to the rate of the transfer of electrons through unit of coupling, and this value is determined by ratio between Eo, ea and eb:
|
(2). |
The transfer of one electron from donor D to acceptor A in subunit "a", is coupled with transmembrane carrying of one H+ and generation of hydrogen ions membrane electrochemical potential. The latter on the electrical circuit (fig. 2) corresponds to the source of voltage em in circuit II, in which the resistance Rah of H+ - pump is also included. The current, flowing in circuit II under action of voltage (ea - em), is equal to the rate of transport of protons by H+- pump of subunit УaФ, and also is equal to current J, flowing through whole unit of coupling:
|
(3) |
The current through subunit "b" is determined as the sum of currents, flowing by chemiosmotic way and in parallel by way of ATP chemosynthesis (fig. 1). In circuit III of electrical circuit (fig. 2) it is shown, that the current J1 on right, chemiosmotic branch (circuit III.1) and current J2 on left, chemical branch (circuit III.2) flow under the action of voltage eb. The sum of currents J1 and J2 through subunit "b" is equal to general current J through whole unit of coupling, i.e., to the current in circuit I:
|
(4) |
The current J1 is coupled with active transport of protons by H+ - pump of subunit "b" and is determined by voltage (eb - em) and resistance of pump Rbh. According to the method of mesh currents, it is possible to write down:
|
(5) |
According to considered two-electron variant of proton-chemical coupling, synthesis of one ATP molecule is coupled with transfer of two electrons and, simultaneously, with transfer of two protons by gradient of their membrane electrochemical potential. So, value of current J2 in circuit III.2 is determined by sum of voltages (eb +em) and by magnitude of ATP-synthase resistance, RA. Beside, ATP chemosynthesis rate and magnitude of current J2 depend on magnitude of phosphate potential ep. This dependence can be reflected by introduction in circuit III.2 of additional source of voltage, ep/2, directed opposite to eb and em. The divider 2 at ep was added due to stoichiometry 1ATP / 2e- per one unit of protonchemical coupling. In this case, the phosphate potential in bulk phase out of mitochondrion was taken as phosphate potential magnitude.
Using the method of mesh currents for circuit III.2, it is possible to write down:
|
(6) |
On the other hand, the value of current J2 in circuit III.2 is equal to 2 of ATP chemosynthesis rate and at the same time, - to the rate of influx in matrix of protons coupled with ATP synthesis.
According to previously published work [16] simple accounts, in case of hypothetical phosphite-thyole mechanism of proton-chemical coupling, rate of ATP synthesis exponentially decreases at DmH+ and DEBA decrease [16], as it is visible from formula (1). In electrical circuit (fig. 2, circuit III) this exponential dependence is reflected by nonlinear nature of ATP-synthase resistance RA, which depends on eb and em in the following way:
|
(7) |
Where RA0 - normalizing multiplier.
The magnitude of DmH+, which is presented in electron equivalent circuits as the source of voltage em, depends on the ratio between rate of pumping out of protons by H+-pumps and proton conductivity of coupling membrane. The circuit IV (fig. 2) reflects that fact, that the rate of pumping out of protons is equal to sum of rates of pumping out through the H+- pump of subunit УaФ (current J in circuit II, fig. 2) and subunit "b" (current J1 in circuit III.1, fig. 2), i.e., J +J1. The proton conductivity, in general case, is conditioned by following processes (see the circuit IV, fig. 2):
The resulting current of protons, coupled with ATP syntheses and phosphorylation substrates transport, is numerically equal to appropriate electron flux J2, according to two-electron variant of proton-chemical coupling. Thus, it is possible to write down, that the summary current, flowing in circuit IV through resistances RU and RL, is equal (J +J1-J2) or, in view of equation (3), is equal 2J1. On the other hand, it is possible to express summary current, flowing through resistance RU and RL, through em:
|
(8) |
The magnitude of phosphate potential, simulated in scheme by source of voltage ep, is determined by ratio between rate of ATP synthesis in coupling unit and rate of ATP hydrolysis in endergonic processes. Let us assume, that all these endergonic processes proceed in extramitochondrial space, where the magnitude of phosphate potential in considered case is determined. The processes of ATP hydrolysis are modeled in electrical scheme by resistance Rg in circuit V. Then in stationary conditions the rate of ATP hydrolysis is equal to the rate of ATP synthesis, i.e. J2/2, and can be expressed as the ratio of phosphate potential magnitude to value of resistance Rg :
|
(9) |
Thereby, we have the system of eight nonidentical equations (1)- (8), in which seven unknown variables (J, J1, J2, ea, eb, em, ep and RA) are present. We transform this system of equations to more convenient kind:
|
(10) |
|
(11) |
| (12) | |
| (13) | |
| (14) | |
| (15) | |
| (16) | |
| (17) |
Where |
The resistances ro, Rah, Rbh, RU, RL, Rg and RA0 reflect the separate parameters of simulated system of energy coupling in real conditions of experiment. Therefore, inhibition of respiration by malonate at succinate oxidation by mitochondria is possible to be modeled by varying of internal resistance ro of voltage source Eo. The addition of uncoupler in incubation media of mitochondria is reflected by varying of resistance RU in definite limits.
The activation of ATP synthesis at decrease of phosphate potential (for instance, owing to addition of ADP or hexokinase in incubation media of mitochondria) is modeled by reduction of resistance Rg.
THE CHOOSING OF THE PARAMETERS OF PROTON-CHEMICAL COUPLING UNIT MODEL
Let us analyze the rates of ATP synthesis and respiration in one protonchemical coupling unit in dependence on DmH+ magnitude, which is changed by two different ways. To set the parameters of system, we take the voltage Eo equal 400 mV, i.e., approximately 1/3 general differences of redox-potentials between oxygen and hydrogen electrodes.
The magnitudes of resistances were chosen taking into account following criteria: range of respiratory control value, maximal degree of activation of respiration by uncoupler, low proton conductivity of coupling membrane and other, including the empirical selection with subsequent computer analysis of model behavior. Resistances chosen below are normalized on one coupling unit and have not absolute, but relative nature, though they are expressed in ohm.
We accept the resistances ro, Rah and Rbh equal 1 ohm. The resistance of natural outflow of protons through membrane, RL, we take equal 100 ohm, i.e., considerably more than resistances of proton pumps. Let's take the ATP-synthase resistance normalizing multiplier RA0 equal 2*1011 ohm (in conditions of ATP synthesis the real resistance RA thus will take order of 10 ohm). We take initial resistance of outflow through uncoupler RU equal 10000 ohm, that approximately can be considered as infinitely large resistance RU in absence of uncoupler. 10000 ohm was taken as initial value of resistance Rg that simulates the respiration state 4 (by Chance).
THE COMPUTER ANALYSIS OF THE CHOSEN MODEL OF PROTON-CHEMICAL COUPLING
The system of equations (10 - 17) cannot be resolved in obvious kind because of existence of nonlinear equation (17), in which variable RA depends on its own magnitude, entering in exponent expression. So the solution was found using computer by method of consecutive approximations on variable RA at the above chosen values of assigned parameters of equivalent electrical circuit. At these conditions, the calculation of necessary parameters - rate of ATP syntheses and rate of mitochondria respiration in dependence on membrane potential - was conducted for two ways of DmH+ change.
The dependence of ATP synthesis rate on DmH+ changed by uncoupler addition was investigated by varying of resistance RU from initial chosen value 10000 ohm to 1 ohm. The lower level of resistance (1 ohm) is chosen two order less than resistance RL of natural proton outflow through coupling membrane. Resistance Rg was taken 1 ohm, that simulates D Gp = 0.
The same dependence on DmH+ changed by addition of competitive inhibitor of substrate SH2 oxidation, was investigated by varying of internal resistance ro in range from 1 ohm (initial value) to 1000 ohm.
Dependence of ATP synthesis rate on DmH+ magnitude for the two considered cases received by computer solution is presented on fig. 3. It is obvious, that the calculated curves exponentially decrease at reduction of membrane potential and are divergent, i.e., the same magnitude DmH+ corresponds to the different magnitudes of ATP synthesis rate. The received data of the computer experiment are on principle agreed with experimental data for mitochondria [6].
|
|
| Fig. 3. Theoretical ATP synthesis
rate (Jp) dependence on membrane potential. Symbols: 1 - titration by the uncoupler; 2 Ц titration by respiratory inhibitor |
Fig. 4. Theoretical
respiration rate (Jr) dependence on membrane potential. Symbols: 1 - titration by the uncoupler; 2 Ц titration by hexokinase |
It is impossible to explain in the frames of chemiosmotic hypothesis the abrupt fall of ATP synthesis rate at insignificant decrease of membrane potential. Even if we admit, that it is consequence of specific kinetic characteristics of ATP-synthase, any case, it isn't possible in frames of chemiosmotic hypothesis to explain the existence of two various magnitudes of ATP synthesis rate at the same magnitude of membrane potential, changed by different ways. However, this effect mathematically strictly follows from the proton-chemical model of energy coupling.
At modeling of dependence of mitochondria respiration rate on magnitude of membrane potential, the change of DmH+ was considered at titration by uncoupler-protonophore, or at titration by hexokinase. Titration by uncoupler, as previously, was modeled by varying of resistance RU from initial value 10000 ohm to 1 ohm. Titration by hexokinase was modeled by varying of ATP hydrolysis resistance Rg from initial value 10000 ohm to 1 ohm.
As the result of modeling two divergent curves were received (fig. 4), that is agreed qualitatively with experimental data [3, 9], which run counter to Mitchell's hypothesis.
The mathematical and electrical models of proton-chemical coupling, considered in present work, permits to receive number of interrelations between other thermodynamic parameters of oxidative phosphorylation system and to explain from single position the large totality of experimental facts, including those, which are in contradiction to Mitchell's hypothesis. The distinctive property of model is the opportunity to receive by calculation and coordination with experimental data the series of such characteristics of energy coupling system, which defy direct experimental measurement.